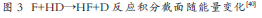化学反应动力学

Dynamics of F+H2 Reaction and Its Isotopic Analogs

        戴东旭(分子反应动力学国家重点实验室(中国科学院大连化学物理研究所) 大连 116023)
        张东辉(分子反应动力学国家重点实验室(中国科学院大连化学物理研究所) 大连 116023)
        杨学明(分子反应动力学国家重点实验室(中国科学院大连化学物理研究所) 大连 116023)

         氟原子,氢分子,化学反应动力学,反应过渡态,非绝热效应

        F atom, H2 molecular, chemical reaction dynamics, transition state of reaction, non-adiabatic effect

        氟原子加氢分子及其同位素分子的反应(F+H2/D2/HD)在化学反应动力学的研究发展中一直扮演着重要的角色。在过去的10年里,科学家们通过精心设计的实验和高精度的理论计算,使得有关该反应体系的态-态动力学研究,特别是对反应机制、过渡态结构及其动力学性质、非绝热效应的认识有了长足的进步,得到了有关F+H2这个教科书式的反应体系动力学行为的结论性的研究成果。

        The reaction of F+H2 reaction and its isotopic variants have played a central role in the development of chemical reaction dynamics. Using improved experimental and theoretical methods, we have made significant advances in the study of the state-to-state chemical dynamics of these reactions in recent years. Strong interactions between theory and experiment have significantly enhanced our understandings of reaction mechanism, transition state, and non-adiabatic effect of these reactions, providing the textbook-like examples of dynamical resonances in elementary chemical reactions.

         任何研究领域都有一个或几个典型的研究案例或研究对象,许多重要的基本规律或现象都是从对这些案例或对象的研究中得到的,对这些研究对象的认识深度代表着该领域的研究水平。氟原子和氢分子及其同位素分子的反应(F+H2/D2/HD)就是化学反应动力学研究领域的一个基本案例[1]。化学反应动力学就是在原子和分子的水平上,用量子力学的语言细致地研究化学反应的动态过程。F+H2体系和最简单的H+H2体系是最早应用于全量子动力学计算的两个化学反应。相对于H+H2反应,F+H2反应不仅更复杂,涉及的研究内容也更丰富,而且还因为该反应对于化学激光有着非常重要的意义,所以F+H2→HF+H和其同位素变体反应在气相化学反应动力学的发展中一直扮演着至关重要的角色。

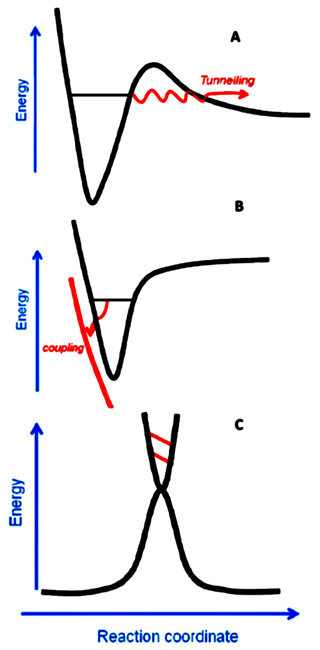
         人们对F+H2反应体系的关注重点是其反应过程中过渡态的性质和动力学行为。过渡态在化学反应中是一个十分重要的概念,它决定了化学反应的速率和微观动力学机制。诺贝尔化学奖获得者John Polanyi和Ahemed Zewail于1995年在Accounts of Chemical Research的Pauling纪念专辑中指出,“直接观测化学反应过渡态”是化学学科的“圣杯”之一[2]。当反应物分子间的碰撞能和某个过渡态的能量相匹配时,反应碰撞截面(总截面或微分截面)就可能出现一个极大值,所以反应过渡态和反应共振密切相关。一般来讲,反应共振可以分为3类(图1):Shape共振、Feshbach共振和势垒(Barrier)共振[3]。Shape共振和Feshbach共振都是由准束缚态与连续态波函数的耦合所引起的。

        Shape共振来源于准束缚态与反应系统同一振动绝热势能面上连续态之间的耦合,而Feshbach共振则来源于准束缚态与不同振动绝热势能面上连续态之间的耦合。如果一个反应在过渡态区域沿反应坐标方向有能量极大值,因而沿反应坐标方向不能存在分立的量子化过渡态,而只能在垂直于反应坐标方向上以最低能量路径为谷地形成分立的势垒型量子化过渡态,这种过渡态被形象地称为量子化瓶颈态(quantized bottleneck state),与此对应的共振称为势垒共振。长久以来,在F+H2反应体系中是否存在反应共振态以及反应共振态的类型一直是化学反应动力学领域的研究热点。

        

        

         有关F+H2反应体系的另一个课题是该反应中非绝热效应的贡献。波恩-奥本海默近似(Born-Oppenheimer approximation)是化学动力学、分子光谱和分子结构等领域广泛使用的基本理论假设[4],又称为绝热近似。该近似在核的质量是电子质量的几千倍的基础上将核运动与电子运动分开,当核的分布发生微小变化时,电子能够迅速调整其运动状态以适应新的核势场,而核对电子在其轨道上的迅速变化却不敏感。在该近似下,处理电子运动时,把核看作是固定不动的,处理核运动时,把电子能量作为核运动的势能。波恩-奥本海默近似不仅使关于分子的电子结构的讨论和计算得到简化,而且使分子势能面的概念得以成立。在波恩-奥本海默近似下,原子核只能在一个绝热的势能面上运动,不同的势能面之间的跃迁是禁戒的。如果化学反应历程在不同的势能面之间有耦合,就是所谓的非绝热效应和过程[5]。对于在基电子态上进行的双分子化学反应来讲,波恩-奥本海默近似在大多数情况下成立,或者说符合绝热近似的反应通道是主要反应途径。氟原子的基态2P因为旋轨耦合分裂成2P3/2(基态)和2P1/2(激发态)两个态。当氟原子和氢分子接近时,这两个态对应着3个不同的势能面,即对应着不同的产物量子态(图2)[6]。对于氟原子和氢分子的反应来讲,在通常的实验条件下,绝热允许的反应通道只有基态势能面,激发态势能面通道由于势垒太高而无法进行。然而在实际的化学过程中,不同的势能面之间常常违反绝热近似而发生耦合,即基态F(2P3/2)对应的势能面的产物有来自于激发态F*(2P1/2)的贡献[7,8]。通常认为,非绝热反应通道对化学反应的贡献相对“正常”的绝热通道小得多[9,10]。但理论计算表明,在低碰撞能下,F+H2反应体系中非绝热通道贡献可能大于绝热通道[11,12],但这一点一直没有得到实验上的确切证实。

        

        

         研究化学反应动力学的基本实验手段是交叉分子束和激光光谱技术。利用分子束技术,我们不仅可以制备速度单色性很好的分子,以进行不同碰撞能条件下的反应散射实验,而且还由于分子束形成过程中的绝热膨胀过程使得分子束中的分子向基态聚集,从而实现从确定的反应物量子态到确定的产物量子态(态-态,state to state)的反应动力学的测量。由于激光光谱技术可以用来制备和探测处于特定的量子态上的分子,因而是现代态-态化学反应动力学实验研究中不可缺少的工具[13,14]。20世纪60年代中期,李远哲等人引入超音速分子或原子束源以及电子轰击电离和飞行时间谱技术,并采用质谱仪作为探测手段,发展出通用型交叉分子束仪器,使得交叉分子束技术得到了广泛的应用和发展[15]。从交叉分子束实验中可以测量产物角分布、产物内能和平动能分布、反应截面与碰撞能及反应物取向的关系等信息,从中推断出化学反应的主要机制、检验势能面的精确度,使我们据此了解化学反应的“原动力”。激光光谱技术的应用使得化学反应动力学的研究得以深入到量子态分辨的层次。激光诱导荧光、共振增强多光子电离(REMPI)、相干反斯托克斯拉曼光谱和红外吸收光谱等已经成为化学反应动力学实验的标准检测手段[16-18]。

         因为所有的检测方法都是测量电信号,所以直接的测量方法就是将产物分子电离。李远哲等人发展的通用型交叉分子束装置采用电子轰击方法电离产物分子,然后转动具有质量分辨能力的探测器来测量微分反应截面。电子轰击电离方法的特点是通用性,即几乎可以电离所有种类的分子,而且电离的几率相近。通用型交叉分子束装置对化学反应动力学的发展起到了极大的推动作用,Herschbach、李远哲、Polanyi也因此获1986年诺贝尔化学奖。

         然而电子轰击电离技术也存在着自身的缺陷。一是由于通用性,导致非信号本底非常大,因而探测区域需要非常高的真空度;二是对探测对象缺乏量子态分辨能力;三是因受电子轰击区域长度的影响,平动能分辨率最高只能达到3%左右。高亮度可调谐激光的采用,促进了共振多光子电离技术的发展。共振多光子电离技术不仅可以检测分子的量子态,而且通过与其他技术的结合,例如离子成像技术(Ion Imaging)[19,20]、多普勒位移(Doppler Shift)[21,22]方法等,可以实现对交叉分子束反应产物的量子态分辨的微分截面的测量。

         共振多光子电离技术是在反应区原位电离产物分子,对于如氢原子这样的轻质量粒子,不可避免地要受到库仑排斥作用、周围空间残余电场等影响,使得平动能分辨率受到严重限制。针对这一问题,20世纪80年代后期,在传统1+1'共振多光子电离技术基础上发展起来里德堡氢原子飞行时间谱技术,该技术为研究与氢原子或其同位素氘原子有关的基元化学反应动力学提供了一个理想的探测方法[23]。该探测方法的第一步是利用Lyman α(121.6nm)光子将氢原子从n=1的基态激发到n=2的第一激发态上,然后再将氢原子从n=2态激发到高里德堡态(n=30—90)。该方法利用里德堡氢原子的长寿命和易被探测的特性来测量化学反应过程产生的氢或氘原子的飞行时间谱。由于一般化学反应过程的氢原子产物没有内能分布,因此通过氢原子产物的平动能分布可以得到伴随产物的内能分布。里德堡氢原子飞行时间谱技术最初被用于研究产物之一为含氢原子的光解反应,并以其高分辨率和高信噪比为这些化学过程的研究提供了很多细节信息,帮助人们理解了一些重要分子的光解反应机理。从20世纪90年代起,该技术与交叉分子束技术相结合[24,25],成为研究化学反应动力学的有力工具之一。

         2004年,我们成功研制了一台分辨率和灵敏度都具有国际领先水平的交叉分子束-里德堡态氢原子飞行时间谱仪[26]。通过引入可转动束源使得反应碰撞能可调、扩大探测角度、降低碳氢化合物真空本底和使用双探测器以提高实验效率,使这台装置成为国际上独一无二的研究产物为氢或氘原子的基元化学反应动力学的最佳实验设备。我们还在该装置中发展出一种新型的双阶脉冲放电氟原子束源,能够产生脉冲宽度更窄、单色性更好且密度更高的脉冲氟原子束[27]。这些实验设备和技术上的创新,使我们能够以更高的分辨率和灵敏度,在分辨产物转动态的层次上测量化学反应的微分截面。在此设备上,我们开展了氟原子加氢及其同位素分子反应的转动态分辨的动力学测量,研究这些反应的共振态结构和动力学性质以及非绝热效应,与全量子散射理论相结合,加深了我们对氟原子加氢及其同位素分子反应这一化学反应动力学领域样板体系的基本动力学过程的认识。

         早在20世纪70年代就有人利用量子动力学计算,预测F+H2中存在共振现象[28-31],但由于所使用的势能面是一维的并且是经验性的,所以不完全确定所预言的共振到底是真实物理现象还是由于近似导致的理论假象。例如Connor在几个势能面上进行了中间络合物几何构型为共线情况下的计算,得到了完全不同的共振态结构[32,33]。20世纪80年代中期,李远哲研究组对F+H2及其同位素分子的反应首次进行了产物振动量子态分辨的交叉分子束实验[34-36],这是一个化学反应动力学领域内里程碑式的实验。他们在实验中观测到,在碰撞能为1.84kcal/mol时,F+H2反应的产物HF(v'=3)的分布出现前向散射峰;在碰撞能为3.32kcal/mol时,F+D2反应的产物DF(v'=4)也出现了前向散射峰。他们认为观测到的前向散射峰可能来自于动力学共振态。鉴于以往的势能面都不能预言实验中的产物振动态和微分截面的分布,Stark和Werner在1996年从第一原理出发构建了高精度的SW势能面[37],但是在SW势能面上所进行的经典散射计算和量子散射计算的对比得出的结论却是否定了HF(v'=3)前向散射峰来自于反应共振态[38,39]。

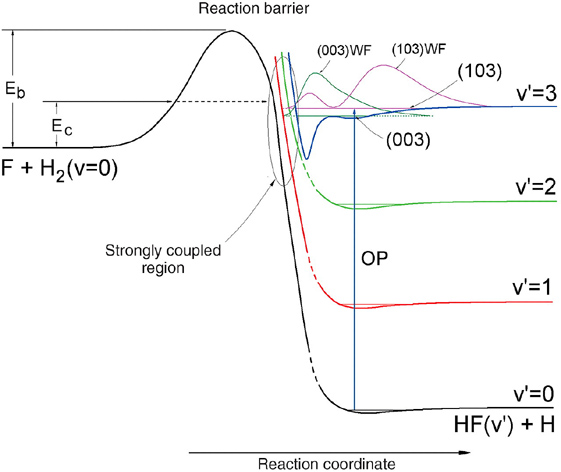
         近年来,实验技术的发展使人们对F+H2反应过渡态有了进一步的发现。2000年,Kopin Liu等人利用多普勒选择(Doppler Selected)离子飞行时间质谱方法对F+HD反应进行了实验研究[40,41]。他们发现,产物HF+D通道的激发函数σR(E)在碰撞能约为0.5kcal/mol处有一个台阶[40](图3);而产物DF+H通道的激发函数σR(E)却没有类似的台阶。在SW势能面上进行的量子动力学计算发现有类似的结果,证实这个台阶是Feshbach共振的结果。然而理论计算的激发函数σR(E)的台阶出现在高于0.5kcal/mol处,而且台阶的高度是实验结果的两倍。Kopin Liu等认为这可能是由这个反应的自旋-轨道耦合的非绝热效应引起的。他们认为F+HD→HF(v')+D反应的共振形成机制是:产物HF(v'=2)的产生是通过HF-D的(003)准束缚态的共振机理进行反应的。但是在F+H2反应中,刘国平等人在实验上并没有发现类似于F+HD的反应共振峰[8]。其他实验化学动力学家们也对这个体系进行了一系列新的研究,但都没有探测到F+H2反应共振的任何新迹象[42,43]。同时,理论上SW势能面存在的一些问题也逐渐被发现,如产物HF(v'=3)的延迟出现、自旋-轨道耦合的影响等。2005年,Skodje研究组在SW势能面基础上构建了一个新的势能面[44](SWMHS-PES)。但是,在低碰撞能区域,该势能面上的反应图像与SW势能面上的图像有非常大的差异,并与实验不符。

        

        

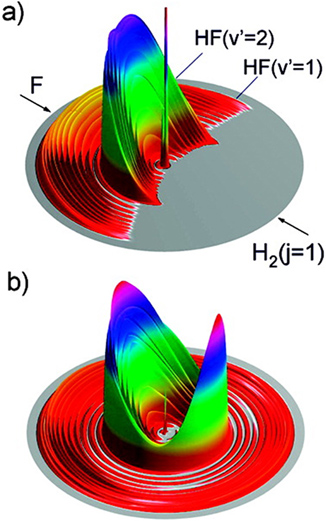
         为了澄清F+H2反应的共振图像,2006年,我们利用里德堡氢原子飞行时间谱方法对F+H2反应进行了全量子态分辨的交叉分子束散射研究[45]。图4是碰撞能为0.52kcal/mol时F+H2(j=0)反应产物HF的转动态分辨的微分截面三维示意图。可以看到在前向散射方向产物HF(v'=2)有一个显著的散射峰。这是在实验上首次在F+H2反应中观测到前向散射峰,如图4(A),之前的实验或者很难达到这样低的碰撞能,或者缺乏足够的灵敏度测量出如此低碰撞能下的产物空间分布。该实验同时观测到HF(v'=2)的前向散射分布随能量的变化在碰撞能为0.52kcal/mol处显示出一个峰值(图5中的圆点)。

        

        

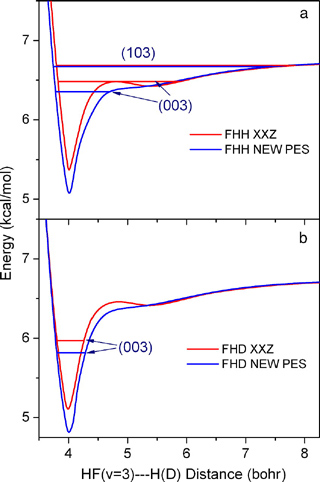
        为了解释这一新的实验现象,理论学家们从第一原理出发构建了一个新的势能面(XXZ-PES)。基于该势能面的全量子动力学计算几乎完美地再现了实验的结果(图4B和图5中的曲线),并清晰地阐述了有关该反应的动力学共振的机理。在XXZ势能面上,HF(v'=3)—H'的振动绝热势存在一个较深的、与反应势垒紧邻的势阱,另外还存在一个浅的范德瓦尔斯势阱(图6)。

        

        

        两个Feshbach共振态,分别为(003)和(103)共振态,就被束缚在HF(v'=3)—H'的振动绝热势阱中。它类似但又不同于SW势能面的图像。从一维波函数的位置可知基共振态(003)主要是束缚在较深的HF(v'=3)—H'的势阱中,而激发态(103)的波函数主要是范德瓦尔斯共振态。基共振态的主要特征类似于在F+HD反应中观测到的共振特征。由于这两个共振态与HF(v'=2)的通道之间存在强烈的耦合,相当于多一个形成HF(v'=2)产物的通道。

        

        

        但是产物HF(v'=2)是前向散射还是后向散射则由中间络合物HHF驻留在两个共振态的时间决定。从实验和理论结果上可以得到结论:处于这两个共振态的络合物大部分衰变为产物HF(v'=2),而且是前向散射,从而造成前向散射的信号比后向的信号强得多。而这两个共振态与HF(v'=0,1)的通道之间的耦合较弱,很难通过这两个共振态打开产物HF(v'=0,1)的通道,因此实验上观测到产物HF(v'=1)的前向散射很弱,而且完全没有观测到产物HF(v'=0)。这正是长期以来人们一直在该反应中努力寻找的Feshbach共振,而且实验和理论取得了完全一致的符合。

         Kopin Liu等人对F+HD反应的研究结果说明这一反应与F+H2反应有着非常明显的差别,即同位素替代对反应共振态有着相当大的影响。当用XXZ势能面对F+HD反应进行动力学计算时发现,尽管相对于SW势能面来讲,依据XXZ势能面计算的共振峰的高度与Kopin Liu的实验结果相符,但在峰的位置上依然存在差别。2008年,我们利用里德堡氢原子飞行时间谱方法对F+HD反应进行了高精度的交叉分子束实验研究[46]。

        

        

        实验发现当碰撞能仅仅变化0.28kcal/mol(98cm-1),该反应的微分截面就发生了剧烈的变化(图7)。这项实验以前所未有的光谱精度(达到几个cm-1的精度)对这一反应的共振现象进行了动力学测量,还对该反应体系的势能面构造和动力学计算提出了苛刻的要求。

         量子动力学计算表明前述XXZ势能面尽管能精确地描述F+H2反应中的共振态动力学现象,但对F+HD反应中的共振态描述却不够理想。图8显示了实验测得的F+HD(j=0)→HF(v',j')+D反应产物HF(v'=2,j'=0-3)的后向信号之和随碰撞能的变化以及在XXZ势能面上进行的量子散射动力学计算结果。该曲线显示出一个明显的共振峰。显然XXZ势能面的计算结果与实验结果有很大差别,计算所得的共振峰位置比实验结果偏移了约0.2kcal/mol。为此我们用CCSD(T)方法重新构建了该反应的一个高精度的势能面(FXZ-PES)[47],从图8可以看出,由新势能面计算的结果与实验符合很好。FXZ在其他动力学性质方面的计算结果也与实验结果符合得很好。当把FXZ势能面应用于F+H2反应体系时,理论计算得到的结果比XXZ势能面的结果更好地符合实验结果。

        

        

        

        

        图9(A)显示的分别是FXZ势能面和XXZ势能面描述的F+H2体系的一维HF(v'=3)—H绝热势阱和共振态。FXZ势能面的基态共振态(003)相对XXZ势能面的向下移动了约0.12kcal/mol,而激发态共振态(103)位置仅仅向下移动了0.01kcal/mol。之前的研究说明,0.52kcal/mol时产物HF(v'=2)的前向散射是(003)态和(103)态两个共振态干涉的结果,而且主要由(103)态决定,因此不难理解两个势能面上的计算均能与实验吻合。图9(B)是这两个势能面分别描述的F+HD体系的一维HF(v'=3)—D绝热势阱和共振态。在F+HD体系中,HF(v'=3)—D绝热势阱只能维持一个基态共振态(v'=3)—D绝热势阱只能维持一个基态共振态(003),而且FXZ势能面的势阱比XXZ势能面的势阱深了约0.3kcal/mol,相应地FXZ势能面的基态共振态(003)也较XXZ势能面的低0.16kcal/mol,所以只有FXZ势能面才能更好地描述F+HD反应体系的动力学。FXZ势能面与F+H2反应和F+HD反应的实验结果高度吻合,说明我们对化学反应动力学的研究无论从实验上还是理论上都达到了前所未有的光谱级的精度。

         尽管我们在2006年通过观测HF(v'=2)的前向散射峰及其随能量变化的共振峰而证实了F+H2反应中共振态的存在及动力学机制,但李远哲等人在1985年观测到的HF(v'=3)前向散射的形成机制还没有给出解答。当时他认为该反应中的前向散射是由F+H2反应中的共振态引起的,但后来的理论研究并不能很好地支持这个说法。2008年,我们利用交叉分子束-里德堡氢原子飞行时间谱技术研究了基态F原子与H2的反应,获得了碰撞能为0.5—1.0kcal/mol的全量子态分辨的微分反应截面[48]。实验发现,产物HF(v'=3)在碰撞能恰好大于反应阈值0.52kcal/mol时就开始产生,然后HF(v'=3)的积分截面随碰撞能增加单调上升,说明产物通道没有出口势垒。图10(A)是产物HF(v'=3)在碰撞能为0.94kcal/mol时的散射微分截面示意图,显示出一个很明显的前向散射峰,这一实验结果与李远哲等人在1985年的实验观测一致。图10(B)是在FXZ势能面上量子动力学计算的结果,理论和实验符合得很好。对于HF(v'=3)反应通道,理论计算表明,在碰撞能为0.94kcal/mol时,总角动量J=10的分波对前向散射贡献最大,J=9的分波的贡献次之,其余分波对前向散射的贡献较小。图11是FXZ势能面得到的HF(v'=3)—H一维振动绝热分波势能面。从图中可以看出,随着碰撞参数的增大,HF(v'=3)反应通道出口处的离心势垒逐渐形成并增大。反应体系在0.94kcal/mol能量下恰好可以隧穿J=10的离心势垒,并且刚好高于J=9的离心势垒。

        

        这说明实验观测到F+H2反应的产物HF(v'=3)前向散射来自于

        反应体系在过渡区域出口处放慢通过HF(v'=3)—H'振动绝热通道上因离心势场形成的势垒所导致的时间延迟。这一结果终于对这一困惑反应动力学领域

        20多年的科学问题给出了一个清晰的答案。

        

        

         现实世界中的化学过程,反应物大多具有一定的转动能,所以研究反应物转动激发对反应动力学的影响具有重要意义。2006—2007年,我们分别测量了F+H2(j=1)反应在0.56和0.19kcal/mol两个碰撞能下的转动态分辨的微分散射截面[49,50]。与前述F+H2(j=0)测量结果所不同的是,F+H2(j=1)反应产物HF(v'=2)在0.56kcal/mol碰撞能下产物分布没有前向散射峰,而在0.19kcal/mol碰撞能下却观测到较大的前向散射峰(图12)。比较F+H2(j=1) 与F+H2(j=0)的产物HF(v'=2)前向散射信号对碰撞能的依赖关系,发现二者比较类似,只是F+H2(j=1)的峰值位置向低能方向平移了0.35kcal/mol,这个数值近似等于H2分子j=1的能级。全量子散射计算的结果也得出了与实验结果相符的结论,说明F+H2(j=1)反应之所以在碰撞能为0.19kcal/mol附件发生共振是因为该碰撞能与H2(j=1)转动能0.34kcal/mol之和符合F+H2(j=0)反应的共振能。

         量子碰撞散射过程的体系总角动量是守恒量,按总角动量分类的量子态称为分波。当发生碰撞的两个原子或分子的自身角动量为零时,碰撞过程的总角动量由碰撞参数决定。两个原子或分子之间发生碰撞从而导致化学反应,其反应机制不仅取决于二者之间的碰撞能,还取决于碰撞过程中的总角动量。很显然,不同的分波在反应过渡态区域中将经历不同的反应共振态,当特定分波的碰撞能的变化接近反应共振态的能级宽度时,实验观测值将仅仅由这个能量范围内的少数几个甚至一个反应共振态决定,因此,对分波共振态的测量将能提供有关化学反应机制的最细致的图像。然而由于反应过渡态寿命非常短(飞秒量级),使得分波共振态在能量上很宽且重叠在一起,因此在实验上很难观测到单个分波共振态的结构。在绝大多数情况下,即使是完全量子态分辨的交叉束实验所测量的微分截面也是不同分波叠加后的平均值,因此,观测单个特定的分波结构是动力学研究领域的一个极大挑战。迄今为止,世界上还没有任何人能够在实验中清晰地观测到这样的分波共振结构。

         根据前述构建的FXZ势能面分析,F+HD反应共振态的寿命长达几百飞秒,这暗示我们有可能探测到单个分波的共振结构。但即使要分辨如此“长”寿命的不同分波的共振态,也必须进一步提高交叉分子束实验的分辨率,以探测由不同分波共振态引起的微分散射截面随能量振荡的现象。在我们使用的交叉分子束-里德堡氢原子飞行时间谱实验装置上,提高实验分辨率的关键是提高HD分子束和F原子束的速度单色性,从而提高碰撞能的分辨率。在前述几项实验中,为了提高H2/D2/HD分子束的速度单色性,我们将H2/D2/HD分子束束源冷却到液氮温度。在本项实验中,我们将HD分子束和F原子束这两个束源都冷却到液氮温度,从而使我们实现了世界上最高分辨的交叉分子束散射实验,其中F原子束的速率比(v/δv:速度与速度分布宽度的比值)为15,HD分子束的速率比为40。通过测量不同碰撞能下的微分散射截面,我们得到了0.9—1.5kcal/mol的产物HF各振转能级的微分散射截面随碰撞能变化的谱图[51]。如图13,

        

        

        反应产物HF(v'=2,j'=6)后向散射微分截面随碰撞能的增加呈现清晰的振荡结构。通过在FXZ势能面上进行的全量子散射理论计算,发现可以将该振荡结构中的三个峰分别归属为F+HD→HF+D反应中J=12、13、14三个分波分别对应的Feshbach共振态。理论预测的共振态能量误差只有0.03kcal/mol,完全达到了需要的光谱精度。

         尽管由于涉及到理论的基本问题,非绝热过程贡献的相对大小是化学动力学领域备受关注的一个课题,但相对于反应共振方面的大量研究来说,关于F(2P)+H2/HD/D2体系中非绝热效应的研究并不是很多,因为理论计算方面需要同时考虑3个相关的势能面,实验方面则需要足够高的分辨率将基态与激发态分别产生的反应信号分开,这些都很难做到。该体系中非绝热效应的理论计算最早可以追溯到20世纪70年代Tully等人的半经典计算[52]。第一个确切的非含时量子散射计算是由Alexander等人在20世纪90年代末做出的[11,12]。他们的计算认为,当碰撞能非常低时,激发态F*(2P1/2)的反应截面比基态F(2P3/2)的反应截面大,碰撞能增大时,F(2P3/2)逐渐占主导地位。最近,韩克利等人用含时量子波包方法也对F(2P)+H2/HD/D2体系中的非绝热效应进行了研究,得到了类似的结论[53-55]。

         实验上关于这个体系的早期研究并没有发现F*(2P1/2)的反应[35,36],第一次清楚给出F*(2P1/2)反应迹象的是Nesbitt等人所做的实验[7,42,56,57],他们发现HF(v'=3)产物布居到F(2P3/2)能量达不到的转动态上。刘国平研究组利用共振多光子电离技术对F+HD反应进行了交叉分子束实验研究[8]。他们给出一定反应能量范围内非绝热效应允许的反应通道的贡献大致占5%—10%。他们的实验存在值得商榷的地方,首先是没有测量F原子束中激发态F原子和基态F原子的相对比例,另外由于受实验条件限制他们没能进行低碰撞能条件下的实验。

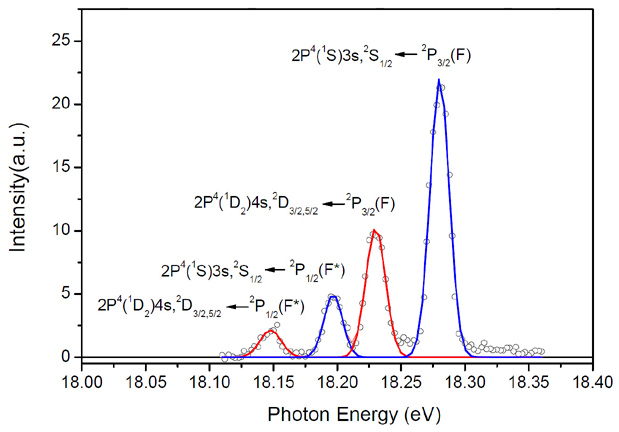
         测量氟原子束中激发态氟原子和基态氟原子的相对比例对于非绝热效应的研究至关重要。由于比较高的电离能,氟原子量子态分辨的检测一直非常困难。1984年,Ruscic等人用氦放电连续光源结合单色仪获得了F和F*的单光子电离谱,并且给出了定量分析[58]。由于He连续谱源光子密度太低,很难应用于超声分子束中。1988年,Aquilanti等人利用Stern-Gerlach磁分析方法获得了F*/F值[59],但此方法分析过程繁琐复杂。1999年,Roth等人发展了3+1共振多光子电离方法探测F和F*[60],但由于缺乏多光子共振截面的准确数据,也无法获得准确的F*/F值。考虑单光子跃迁截面比较容易计算,实验中对光强的关系也易于校正,加之Ruscic等人的结果给出的谱线较为清晰明确,所以我们决定以同步辐射光取代Ruscic等人实验中的He连续谱光源,通过测量氟原子的单光子电离光谱来确定脉冲氟原子束中F*和F的比例。测量F(2P3/2)∶F*(2P1/2)的实验是在合肥的国家同步辐射实验室原子分子物理实验站进行的。由我们自行设计研制两级脉冲放电装置产生的脉冲氟原子束与同步辐射光相交,氟原子通过吸收682?左右的同步辐射光从2P3/2和2P1/2两个量子态跃迁到两个自电离态[2P4(1S0)3s,2S1/2]和[2P4(1D2)4s,2D3/2,5/2]并随之发生自电离。图14是实验得到的氟原子单光子电离光谱,左边两个较弱的峰为激发态F*原子的跃迁谱线,右边两个较强的峰为基态F原子的跃迁谱线,分别对应着相同的上电子态。由此我们可以准确推算出我们使用的脉冲放电氟原子束中F与F*的比率为4.8。

        

        

         我们用相同的F原子束源与D2分子束进行交叉分子束实验,用里德堡氘原子飞行时间谱方法测量转动量子态分辨的反应截面。我们使用的实验装置所具有的高分辨率足以使我们在能量上区分开非绝热和绝热两个反应途径的产物,再由前述测得的F与F*的比率,我们就得到了F+D2反应中非绝热通道与绝热通道的贡献数值。通过改变碰撞能,我们还可以进一步得到二者的贡献随碰撞能的变化关系[6]。如图15,其中分离的点为实验结果,曲线为Alexander等人计算的结果。图15(A)为F*(2P1/2)+D2(j=0)与F(2P3/2)+D2(j=0)反应的积分截面,可以看出二者均随碰撞能的增加而增加,但后者比前者增加快,这与理论预期完全相符。图15(B)为F*(2P1/2)与F(2P3/2)反应截面比率,可以看出该比率随碰撞能的增加而减小,在碰撞能低于0.5kcal/mol时,F*(2P1/2)反应性比F(2P3/2)大,说明在低碰撞能下,F*(2P1/2)起主导作用。在0.25kcal/mol的时候,F*(2P1/2)的反应性甚至达到F(2P3/2)反应性的1.6倍,说明在低碰撞能下玻恩-奥本海默近似在氟加氘反应中完全失效。

        

        

         经过近几年的努力,人们现在对F+H2这个化学反应动力学领域中教科书式的样本体系的反应过程、过渡态结构及其动力学性质、非绝热效应等有了非常深入的认识。F+H2及其同位素变型反应是一个典型的存在动力学共振态的反应体系,但在这个反应体系中却存在不同的共振机制。在较低反应能时,主要是HF(v'=3)—H势能面上的两个反应共振态在起作用;在较高的反应能时,则是因为HF(v'=3)—H产物出口通道的离心势垒导致产物HF(v'=3)发生前向散射。在较低碰撞能下,F+D2反应中非绝热效应的贡献要比绝热近似允许的反应通道的贡献要大,即波恩-奥本海默近似在该反应低碰撞能时是失效的。随着碰撞能的增加,绝热近似允许的反应通道的贡献比非绝热效应的贡献更快地增大,并逐渐占据主导地位。

         从本文我们可以看出,实验和理论的相互作用推动了F+H2及其同位素分子反应体系的化学反应动力学研究的发展,实验通过新现象的发现指导理论构造更为精确的势能面,而更为精确的理论帮助实验发现新现象,并可进一步推动理论的发展。通过这一系列的理论和实验结合的紧密互动,使得我们对该反应体系的认识上升到了一个新的境界。